Over View of Buckling of Struts
Buckling of strut is an important phenomenon in engineering. In this experiment buckling of struts for different materials has been studied. Materials used in this study were aluminum, steel and brass.
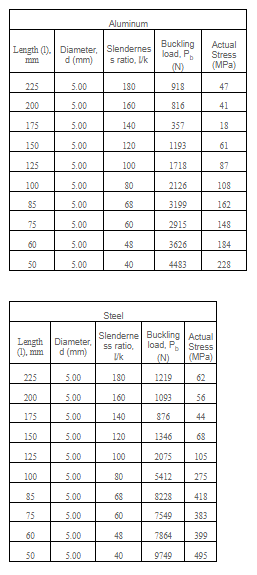
Ten samples of circular struts of similar diameter but of different length were taken for each material type.
Tensile testing machine was used to perform the experiment. Two different methods were used to find the buckling load and stress theoretically.
Euler formula which is usually used for long struts was used to calculate the amount of buckling load and stress in the samples.
Rankine’s formula was also used to calculate the load and stress in all the samples of different materials.
The data for experimental, Euler’s formula and Rankine’s formula was then gathered, manipulated and put in tabular form to make it eye-catching and easily understandable.
Graph for all materials show that value of stress is very close to experimental values at high slenderness ratio while the difference in the value of stress is quite large at low slenderness values.
Aim
“To Study the Buckling of Struts”
The aim of this experiment is to study different techniques to measure buckling of struts made up of different engineering materials.
Two methods from theory are also used to calculate the amount of buckling load and stress. The materials included in this study are brass, steel and aluminum.
Objectives
In order to complete the experiment of buckling of struts, the following pieces of work will be completed in the given order.
- Gathering data from the apparatus to complete the test log sheet
- Calculation of buckling load using Euler’s theory
- Calculation of buckling load using Rankine’s theory
- Comparison of experimental and theoretical value for each material
- Discussion on the results
Theory on Buckling of Struts
Basics of buckling and struts
Struts are an important engineering component found in different engineering applications usually installed to bear compressive loads. They can also be used to take tension loads.
In theory, there are two theories for studying buckling in the struts. One of which is Euler’’s theory and the second is Rankine’ formula.
Formulas and important parameters used in both theories are discussed one by one.
Euler Formula for Buckling
Euler Buckling Theory is a classical theory to find the critical buckling load for the column of any cross-section.
It is usually adopted to calculate the buckling load in long columns.
The derivation of Euler’s formula for buckling starts from noting that bending moment in a loaded column and buckled column is ‘Py’.
Where ‘P’ is the load applied and ‘y’ is the deflection of strut or column.
This expression is then put into beam deflection equation and appropriate boundary conditions are then applied which leads to the final formula of Euler’s theory of buckling.
Euler’s formula for calculating the buckling load is given as
P_E=(π^2 EI_min)/(L_e^2 )
Where
‘P_E’ is Euler’s load (Buckling or Crippling) or sometimes known as critical load. It is called critical because increasing load beyond this value will cause the strut or column to buckle. ‘E’ is the Young’s Modulus of column’s material.
This value will change for all materials. ‘I_min’ is the minimum moment of inertia for a column’s cross section.
Suppose if the column is rectangular, the moment of inertia for the smaller side will be put into the formula. Because column bends in the direction of smaller dimension.
But in our study, we are using a circular column, so there will be only one moment of inertia. L_e is the effective length of the column that actually takes part in bending.
Sometimes, it may happen that complete length of the column does cause bending.
Euler’s stress can then be calculated by simply dividing P_E by the cross-sectional area of the strut or column.
Rankine’s Formula for Buckling
Rankine’s theory for finding buckling load on strut is used to calculate buckling load in the columns of short, average and large length.
The column is decided to be short, medium or long based on the l/k ratio. The derivation of Rankine’s formula starts from the statement
1/P_R =1/P_E +1/P_c
Where P_R is Rankine’s crippling or buckling load, P_E is Euler Buckling load and P_c is crushing or compressive load.
For the small sized struts or columns, 1/P_E becomes almost equal to zero so the Rankine’s buckling load will be equal to P_c.
Similarly, for the long struts or columns 1/P_c becomes almost equal to zero and the Rankine’s buckling load will be equal to P_E.
The mathematical manipulation of above equation leads to the following form of Rankine formula,
P_R=(σ_c A_c)/(1+a〖(Le/k_min )〗^2 )
Where σ_c compressive load, a is the Rankine’s constant whose value will change depending upon the material of the column.
Procedure of Buckling of Struts
- The experiment to find the buckling load is performed on tensile testing machine. Following set of steps are to be performed to complete the experiment.
- First of all, length of column is measured using micrometer or simple steel ruler and value is recorded in mm.
- Cross-sectional area of the each specimen is then calculated from the radius of specimen.
- After that, specimen is placed between the jaws of the machine as per the instructions provided and the buckling test is performed.
- The value of load is printed for each person in the group.
- The value of load is recorded in N (Newton).
Experimental Results
Discussion on Buckling of Struts
Actual stress, stress using Euler’s formula and Rankine’s formula for Aluminum, steel and brass respectively has been found in this experiment. Figure-1 shows the graph between slenderness ratio and buckling stress for aluminum.
The results of rankine’s theory are closer to the experimental values at higher slenderness values but initially the error is quite high as initial stress value for Rankine Formula is very low as compared to that of the experimental value.
While results of Euler’s theory are closer to experimental values at high slenderness ratio but the error is quite high at low values of slenderness ratio.
The result provided by the Euler’s theory area non uniform as the graph show sudden increase and decrease in the stress value for increasing value of slenderness ratio.
This sudden increase and decrease can only be explained in way that either stress production depends highly on material properties like strength, hardness and ductility or the experimental setup has limitations for this method.
It also shows that with increasing value of slenderness ratio the stress produce in the truss start to decrease.
The graph pattern of stress and slenderness ratio is non-linear which show that it depends a lot on other material properties rather than just on the specimen dimensions or slenderness ratio.
Sources of Errors
- Any slippage in grip can distort the measurement.
- Axial misalignment of machine jaws can cause error.
- The large error at low values of slenderness can be due to fact that the grip weight might be ignored
Conclusion on Buckling of Struts
The aim of this experiment was to study different techniques to measure buckling of struts made up of different engineering materials.
Two methods from theory were used to calculate the amount of buckling load and stress. The materials included in this study were brass, steel and aluminum.
The results of rankine’s theory are closer to the experimental values at higher slenderness values but Euler’s theory are closer to experimental values at high slenderness ratio but the error is quite high at low values of slenderness ratio.
It was concluded that Euler’s theory demands extra strength for material which can boost the costs while Rankine’s theory underestimates the material’s strength which can cause serious problem in real life structures.





No comments:
Post a Comment