Buckling of Strut Lab Report

In construction applications a column or strut is an element that is used to withstand compressive load. 

Strut is similar to beam but it is used in vertical position and normally horizontal beams are placed on the columns or both ends of beams are rested on two struts on either end of the beam. 

struts are usually designed to withstand high compressive loads and they can fail or buckle if the loads are too large and columns are unable to withstand that load. 

Normally the load at which the column buckles is called critical load and strut is typically designed to be used well below this critical load.

However, even if the structure is subjected to small loading well below  critical buckling load of strut, the continuous application of such loads could eventually fatigue the structure and build up to buckling failure. 

Therefore, understanding the buckling of strut, its characteristics and designing in safety factors are important. In this experiment we will see how columns buckles ate different loads when their ends are fixed or pinned.

Calculating the Buckling of Strut 

The following dimensions of the strut were measured for rectangular strut

Width, b = 100 mm

Depth, d = 50 mm

For rectangular shape column the second moment of area can be calculated as

Second moment of area

I =(bd^3)/12

Putting in values

Second moment of area 

I = 0.05*(0.1)^3/12  = 4.16* 〖10〗^(-6)   m^4

The buckling load for buckling of struct can also be calculated using Euler equation where it can be seen that the buckling 

load only depends on the cross sectional area, material properties such as Young’s modulus ‘E’ and the way both ends are fixed. 

The Euler equation is given by

P =πEI/kL

Where the value of ‘k’ depends how the ends are fixed.

For Pin End Connection

If both ends are pinned then ‘k=1’ will be taken. 

P =πEI/kL

P =(3.14*97*〖10〗^9*4.16* 〖10〗^(-6))/(1*L)

P =272 N

For both fix end connections

P =πEI/kL

P =(3.14*97*〖10〗^9*4.16* 〖10〗^(-6))/(0.5*L)

P =1129 N

If one end is pinned and the other end is fixed then ‘k=o.7’ will be taken. 

P =πEI/kL

P =(3.14*97*〖10〗^9*4.16* 〖10〗^(-6))/(0.7*L)

P =570 N

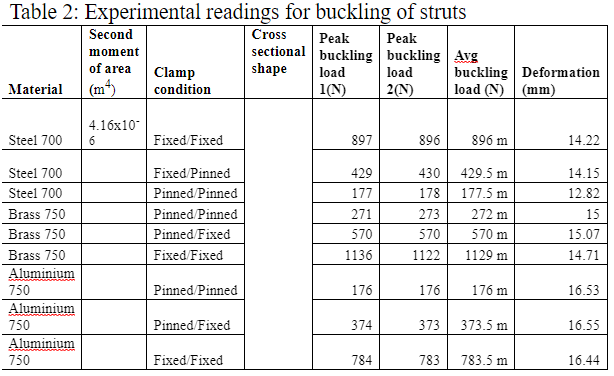experimental reading for buckling of strut

Discussion on Buckling of Strut 

From the results given in table 2 it can be seen that different struts buckle at different critical loads. The buckling depends on many factors such as the material by which the column is made of and the way by which both ends are fixed or pinned. 

In this case it is assumed that all struts have similar cross sectional areas and therefore have constant value for second moment of area. The columns made of brass and aluminum will have different values of ‘E’ but same value of second moment of area ‘I’ if the cross sectional area is same. 

From table 2 readings it is clear that the struts can take larger loads before knuckling when both ends are fixed. Same is true for aluminum and brass columns. The young’s modulus of brass is 97 G Pa while for Aluminum it is 69 MPa. 

If the second moment of area is same for both struts then the column made of brass should take larger load before buckling given that both ends are fixed for both struts. From table 2 it is clear that the column made of brass buckles at 1129 N load while the strut made of Aluminum buckles at 783.5 N when both ends were fixed. 

From Euler equation it can be seen that the buckling load will be directly proportional to the young’s modulus of the material the strut is made of. Therefore brass is more durable and can withstand higher compressive loads. 

Concluding the Buckling of Strut 

For strut design the maximum bending stress was calculated and also keeping in mind the safety factor the design stress was calculated. It was concluded that the material should be used with yield stress of 75 MPa for a safe design of strut. 

For strut design the aluminum and brass strut were tested and it was seen that the brass strut has larger capacity to withstand compressive loads for similar cross sectional area and end fixing. 

By considering the calculations given in this report more suitable columns can be designed to be used in underground construction for London underground tunnels.