VENTURI METER AND ORIFICE PLATE LAB REPORT

Venturi meter effect and orifice plate effects are two main and very important phenomena in the fluid mechanics sub-field of mechanical engineering. 

In this post, the effect of the venturi meter and orifice plate on the fluid flow will be discussed and complete work will be presented in the form of a report. 

Aim

This experiment aims to study the overall meter coefficient C of the Venture meter and Orifice plate

Objective

The objectives of this experiment are

1. Understand the effect of a decrease in the area on the velocity and pressure of the flowing fluid

2. Understand the relationship between velocity and pressure of flowing fluid

3. Find the meter coefficient for the venture meter and orifice plate

Venture Meter

According to Michael Reader-Harris (n.d), a Venture meter is an instrument used to study the flow of fluid when it passes through the converging section. 

There is an increase in the velocity and decrease in the pressure of the flowing fluid when the area available to flowing fluid decreases, this effect is called the venture effect named after the physicist who first introduces this theory. 

Orifice Plate

According to Michael Reader-Harris (n.d), an Orifice plate is an instrument used for three different applications one to measure the flow rate, second to restrict the flow, ad third to reduce the pressure of the flowing fluid. 

It depends on the orifice plate-associated calculation method that either the mass flow rate or the volumetric flow rate is used for calculation. 

It uses the Bernoulli experiment which shows the relationship between velocity and pressure for a flow of fluid. When one increases then the second one decrease.

Study the complete Bernoulli experiment and the Effect of the Sluice Gate on the Flow of Fluid

According to DANIEL MEASUREMENT and control white papers, the following are the different types of orifice plates

• The Thin Plate, Concentric Orifice
• Eccentric Orifice Plates
• Segmental Orifice Plates
• Quadrant Edge Plate
• Conic Edge Plate

Theory of Venturi Meter and Orifice Plate

According to Miller, R.W (1996) principle of continuity state that the decrease in the area of the flowing fluid will increase the velocity of the flowing fluid. 

With this increase in the velocity of the fluid, the fluid pressure will decrease to conserve mechanical energy according to the law of conservation of energy. 

Flow rate is the product of the velocity of the flowing fluid with the area from which the fluid is flowing. In the venture meter, the area of the tube decreases gradually due to which the velocity increase to keep the flow rate constant. 

In the orifice plate, there is a sudden decrease in the area of the flow due to the restriction of the orifice plate. Due to this velocity will increase and pressure will decrease.

According to Bernoulli’s equation

P1+  1/2×ρ×v1^2+ ρgh1=P2+  1/2×ρ×v2^2+ A

A the change in height is zero so

P1+  1/2×ρ×v1^2= P2+  1/2×ρ×v2^2

P2 - P1=  1/2×ρ×〖(v〗1^2- v2^2)

As we know

Q=AV

Q=A √((2(P2-P1)/ρ)/(〖[A1/A2]〗^2-1))

As we know

P= ρgh

So

Q= A1 √((2×g × ∆h)/(〖[A1/A2]〗^2-1))

In above equation 

Q is the flow rate

A1 is the area before the convergence

A2 area of convergence (throat)

∆h is a difference in height of heads across the convergence

For real fluid, there will be differences in the theoretical and measured values this may be due to the meter coefficient C

Q= C ×A1 √((2×g × ∆h)/(〖[A1/A2]〗^2-1))

Apparatus

Orifice Tube and Venture Meter

Supply Hoses

Measuring Tank

Procedure Venturi Meter and Orifice Plate

To set up the orifice tube and venture meter apparatus two tubes were connected one on each of the outlet and inlet of the apparatus. 

The tube which was connected to the venture meter outlet was further connected to the measuring tank. 

To level the orifice meter and venture tube apparatus, adjustable screws are provided at the apparatus.

The apparatus was connected to the power source to run the motor for the water supply. The bench valve and the control valve of the apparatus were open to let the water move into the tube and to remove all the air pockets.

To raise the water level in the manometer tubes the control valve was closed gradually and when the height of the water level was enough high then the bench valve was gradually closed. 

With both valves closed there was static water in the meter at a moderate pressure

The flow rate of the water was recorded and the height of the water level was also recorded in all the tubes

The difference between the heights of the water level and the flow rate will change upon opening any one of the apparatus valves. 

The flow rate was calculated by noticing the time required to fill the tank of a known weight and at the same time the level of the water in the manometer tubes was also recorded

The same process is repeated for different flow rates

Sample Calculations for Venturi Meter and Orifice Plate

Mass = 6 Kg

Volume = 6/1000 = 0.006 cubic meter

Time = 12.81 sec

Flow Rate = 0.006/12.81 = 0.0004684 cubic meter/sec

For Venturi Meter

  

 C=  Q/A_1 ×1/√((2×g × ∆h)/(〖[A_1/A2]〗^2-1))

C = (0.0004684/0.053066)×  1/√((2×g × 0.267)/([26/16]^4-1))

C = 0.00943

Experimental Results Venturi Meter and Orifice Plate

Discussion Venturi Meter and Orifice Plate

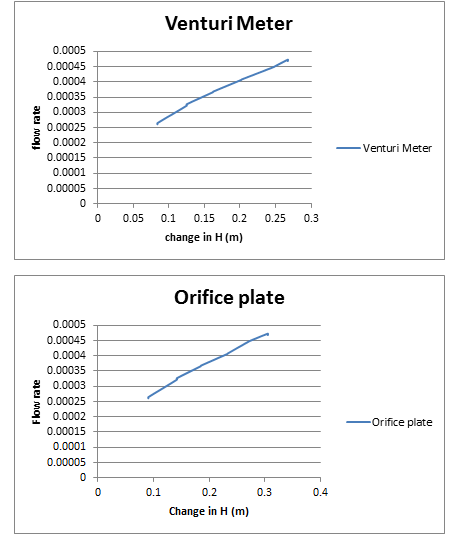
1. Curve shown in the graphs shows the linear relationship between flow rate and difference in height

2. Result shows that with a decrease in the flow rate, the value of the ∆h also decreases. So it can be said from the results that the difference in the height of the water level is directly proportional to the flow rate.

3. Change in the height of the water column of the venture meter is much less than the change in the height of the water column in the orifice plate this is because the difference in diameter of the areas of the orifice is much more than the venture meter. 

So we can say that the difference in height of the water column is directly proportional to the difference in the diameter of the area.

Conclusion Venturi Meter and Orifice Plate

An experiment was conducted to find the overall meter coefficient C in the venture meter and orifice tube and results show that the flow rate and ∆h are directly proportional to each other and along with this ∆h and the ∆d are also directly proportional to each other. Both these things are important as they are used to calculate the overall meter coefficient C

References

1. Michael Reader-Harris (n.d) Chapter 2 Orifice plate, Orifice Plates and Venture Tubes, Spring
2. Miller, R.W (1996) Flow Measurement Engineering Handbook 3Rd ED. McGraw-Hill Book, New York N.Y
3. USBR (1996) Flow Measurement Manual. Water Resource Publication LLC Highland Ranch Co 
4. Michael Reader-Harris (n.d) Chapter 3 Venture tube, Orifice Plates, and Venture Tubes, Spring