Deflection of Beam Lab Report

1.0 Aim Deflection of Beam Lab Report

Aim of this lab work is to study and understand the deflection of beam made of different materials

2.0 Objective Deflection of Beam Lab Report

Study and understand different types of beams

Study and understand the permissible load of different beams

Study and understand the effect of beam material on deflection of beam

Study and understand the effect of beam geometry of beam bending

3.0 Introduction to Deflection of Beam Lab Report

3.1 Beams

According to Dr. R. K. Bansal (n.d) a structural element which is used to support heavy loads in different structures is called beam. 

Beam in any structure bears huge load which tries to bend the beam and beam support the structure by resisting the bending produce by the load. 

Ability of the beam to resist the load depends on the type of beam, material of beam and shape of beam, S Timoshenko (1940). 

According to  there are many different type of beam and each one of these beams can be of any material and can of many different shapes.

Some different types of beam are describe below

Simple supported beam

Simple supported beam is one which has support at its both ends but does not face any moving resistance

Fixed beam

Like simple supported beam fixed also has support at its both ends but fixed beam has moving resistance 

Over hanging beam

Over hanging beam also have support at both of its ends like simple supported beam but one of its ends is free and extended further from the end support

Double over hanging beam

Double over hanging beam is just like over hanging beam, the only difference is that its both ends are extended beyond the end support

Continuous beam

Continuous beam is one which has large length and it is supported by more than two supports

Cantilever beam

Cantilever beam is one which has its one end fixed and other end is free to vibrate

Trussed beam

Trussed beam is a special type of beam which has increased strength due to additional rods and cables in beam

In this experiment only two types of beam will be discussed one is simple supported beam and other is cantilever beam. 

Talking about the material of the beam, in this lab experiment three materials brass, aluminum and steel will be discussed.

3.2 Elastic Modulus 

Elastic modulus is the mechanical property of material which is the ratio of tensile stress and strain. 

Greater the value of the elastic modulus stiffer the material is and lower value of elastic modulus means the material deflect a lot at small stresses, M. F. Ashby (2010).

E=σ/ε

Where 

E is the Elastic modulus

σ = stress

ε = strain

3.3 Deflection

According to John Case (1999) when a body is under stress, then that stress tries to change its shape and dimensions. 

Change is shape of the body is called deflection and change in the dimensions is called strain. 

Following is the equation which can be used for calculating deflection in beams

δ=(FL^3)/KEI

Where

F is the force

L is length of beam

K is constant based on the position

E is elastic modulus

I is second moment of area

3.4 Permissible Load

Permissible load is the maximum amount of load which can be applied in the on to the beam it is also called the allowable load, Ferdinand P. Beer (n.d). 

This load shows the strength of any beam with respect of the load applied on it. It is very important to calculate the permissible load of all the beams in order to get a safe structure. 

According to P. Beer (2012) permissible load can be calculated with the help of Flexure formula whose equation is as follow

σ=My/I

σ=(F*x*y)/I

Where

F is the permissible load 

σ is the maximum value of stresses for material yield strength

x is the distance from the fixed point of beam to point of application of load

y is the Distance from the neutral axis to the point of interest

I is second moment of inertia or area

4.0 Procedure

Following is the procedure which was adopted to perform this experiment

• First of all the apparatus was setup and beam was placed on it
• Second the dial gauge was placed on its placed
• Third weight pan was placed and weight was placed on it
• Reading was taken for each and every increment of weight
• Value was properly arranged in the tables
• Procedure was repeated for different beams and different spans 

5.0 Dimensions of beams

5.1 Brass

Length of beam = 30 cm = 0.3 m

Cross section height = 0.31 cm = 0.0031m

Cross section width = 0.95 cm = 0.0095mm 

5.2 Aluminum

Length of beam = 30 cm = 0.3 m

Cross section height = 0.31 cm = 0.0031m

Cross section width = 0.95 cm = 0.0095mm

5.3 Steel

Length of beam = 30 cm = 0.3 m

Cross section height = 0.31 cm = 0.0031m

Cross section width = 0.95 cm = 0.0095mm

6.0 Simple supported beam calculations

6.1 Calculations for permissible load at 1/2 span

Flexure Formula

σ=My/I

σ=(F*x*y)/I

σ=11 MPa

Distance from the fixed point to application of force= x=0.15 m

Distance from the neutral axis to the point of interest y=0.00155

Second moment of inertia = I=1/12 bh^3=(0.0098*〖0.0031〗^3)/12=2.358*〖10〗^(-11) m^2

F=(11*2.358*〖10〗^(-11))/(0.15*0.00155)=(2.585*〖10〗^(-10))/(2.325*〖10〗^(-4) )=1.11 N

6.2 Calculations for permissible load at 1/4 span

Flexure Formula

σ=My/I

σ=(F*x*y)/I

σ=11 MPa

Distance from the fixed point to application of force= x=0.0075 m

Distance from the neutral axis to the point of interest y=0.00155

Second moment of inertia = I=1/12 bh^3=(0.0098*〖0.0031〗^3)/12=2.358*〖10〗^(-11) m^2

F=(11*2.358*〖10〗^(-11))/(0.075*0.00155)=(2.585*〖10〗^(-10))/(1.1625*〖10〗^(-4) )=2.2262 N

6.3 Calculation for Elastic Modulus at ½ spans

δ=(FL^3)/48EI

E=(FL^3)/48δI

Force = F = 1.96 N 

Length = L = 0.3 m

Deflection = δ = 2.21 mm = 0.00221 m

E=(1.96*〖0.3〗^3)/(48*0.00221*2.358*〖10〗^(-11) )=( 0.05292)/(2.5*〖10〗^(-12) )  

E= 2.1168*〖10〗^10 Pa

6.4 Calculation for Elastic Modulus at 1/4 spans

δ=Fa/48EI(3a^2-4l^2)

E=Fa/48δI(3a^2-4l^2)

Force = F = 1.96 N

Length = L = 0.3 m

Deflection = δ = 2.21 mm = 0.00045 m

E=(1.96*0.00075)/(48*0.00045*2.358*〖10〗^(-11) )(3*〖0.3〗^2-4*〖0.00075〗^2) 

E= 14327462781 Pa

7.0 Results of Deflection of Beam Lab Report

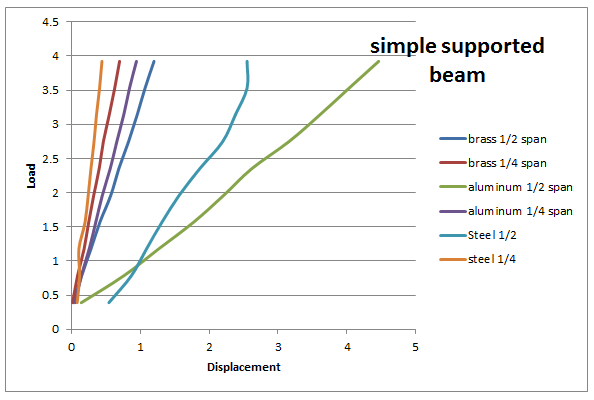
Experiments were performed on simple supported beam and cantilever beam made of three different material brass, aluminum and steel. Data of experiments was written in their respective tables. With the help of the data collected from the experiment graphs were prepared for each and every case and all those graphs are mention below.

7.1 Elastic Modulus of Different Material

8.0 Discussion on Deflection of Beam Lab Report

Six different experiments were performed to study and understand the deflection of simple supported beam and cantilever beam and results are been shown in two tables and six graphs in result section. Now each graph will be discussed here.

• First graphs for simple supported beam made of brass and the values show a liner relation between load and displacement in ½ spans and ¼ spans. 
• Values of the displacement of bam for brass is greater than steel because according To Kenneth G. (2010)  brass is more ductile than steel have lower value of elastic modulus
• Second graph of aluminum shown the similar trends like the brass graphs. 
• It also has liner response between load and displacement but its value of displacement for the given load is more than that of the brass which shows that aluminum is more ductile than that of brass as explained by B. K. Agrawal (2007). 
• The third graph of steel has very graph of brass and steel and has linear response for both spans but its values of displacement at the given load is smallest from other two which show that steel is less ductile than other two and has highest value of elastic modulus and this property is being proved by George Murray (n.d).
• Brass graph for cantilever show similar trends of first graph but in this graph value of displacement for both spans are very different. ¼ span show very little displacement with respect to the ½ span under the same load 10 as explained by Daniel D.
• Pollock (n.d). Aluminum graphs for cantilever has the trend as of brass graph but the values are very different. 
• Like brass graph ¼ span show very little deflection where ½ span show large deflection under the same load, Charles Gilmore (n.d). 
• Steel graph for cantilever show very abnormal values of displacement. ¼ span of steel shows only 0.4 mm deflection at the highest load and ½ spans shows 2.5 mm deflection at highest load

According James M. Gere (n.d) to the equation of deflection, second moment of inertia of the beam which is the property of the beam related to its shape and dimension has very important role in deflection of beam. 

Beam with high value of second moment of inertia or second moment of area will show less deflection and beam with low value of second moment of inertia will show larger deflection. 

From this it can be concluded that the second moment of inertia is property of beam which resist the bending or deflection of beam. 

According to the table the value of elastic modulus for brass is about 37.5 GPa whereas the value of elastic modulus in books is 105 GPa which is almost three time the value obtain from the graphs or experiments. 

Like that for aluminum the value of elastic modulus is almost 26 GPa which is almost 2.5 times less than the book value of 69 GPa. For steel the elastic modulus value is about 29 GPa which more than six time less than the book value of 200 GPa. 

According to Raymond Aurelius Higgins (1994) there is a great different in values of elastic modulus, which shows that there are some errors in the experiment and those errors needed to discussed in order to get accurate values for elastic modulus.

Error in the beam experiments could be form two sources one in apparatus error and second is human error. Instrument error includes inaccurate dial gauge, apparatus not balance on horizontal surface or beam is already deformed. 

A personal error includes observation and calculation with wrong method or lack of experience in experimentation. 

Error in apparatus which is also known as instrument error can easily be find out by repeating a certain experiment over and over again if all experiment show inaccurate value means apparatus has some errors. 

It can be removed by calibrating it with a good standard apparatus. Personal error can find out by repeating the experiment with some experience person and can be removed by practices.

 

9.0 Conclusion on Deflection of Beam Lab Report

Aim of studying and understanding the different types of beams and effect of different factors in deflection of beam has been completed successfully. 

Six experiments were performed on two different types of beam under tow different conditions and result where plotted on graphs and were discussed in details. 

From these experiments it can be concluded that the deflection in a beam under a constant force depends on its type, shape, material and point of application of force. 

It can also be concluded that the experimental elastic modulus of same material is different in every case and really depends on the beam type, shape and loading place.